今天有人问我一个数学问题:
“在由数字1、2、3、4、5组成的所有没有重复的5位数中,大于23145且小于43521的数共有多少个。”
最初想了想用排列组合的思想做,试算发现数量超过10个!!
天呀,那么多!超过十个的事情就交给计算机算吧,于是放弃数学方法,改用Javascript解决。
首先尝试把重点放在五个数字的排列上,后来发现写出五个数字排列的算法还不如写出验证所合成的五位数的有效性来得简单,于是有了如下的程序:
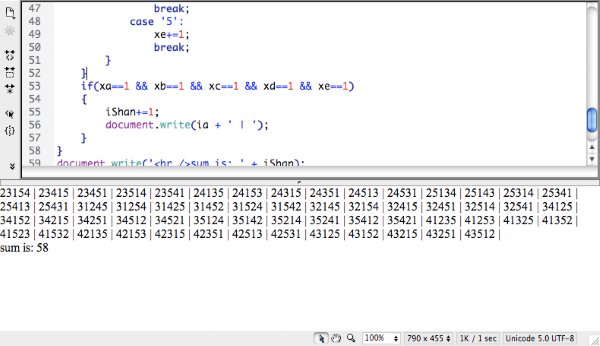
程序输出的结果如下:
23154 | 23415 | 23451 | 23514 | 23541 | 24135 | 24153 | 24315 | 24351
| 24513 | 24531 | 25134 | 25143 | 25314 | 25341 | 25413 | 25431 |
31245 | 31254 | 31425 | 31452 | 31524 | 31542 | 32145 | 32154 | 32415
| 32451 | 32514 | 32541 | 34125 | 34152 | 34215 | 34251 | 34512 |
34521 | 35124 | 35142 | 35214 | 35241 | 35412 | 35421 | 41235 | 41253
| 41325 | 41352 | 41523 | 41532 | 42135 | 42153 | 42315 | 42351 |
42513 | 42531 | 43125 | 43152 | 43215 | 43251 | 43512 |
sum is: 58
PS:由于我特别粗心大意,不知道程序有没有其他错漏。呵呵,我完成调试的环境是:Mac OS X Leopard 10.5.6 + Safari 3.2.1
“在由数字1、2、3、4、5组成的所有没有重复的5位数中,大于23145且小于43521的数共有多少个。”
最初想了想用排列组合的思想做,试算发现数量超过10个!!
天呀,那么多!超过十个的事情就交给计算机算吧,于是放弃数学方法,改用Javascript解决。
首先尝试把重点放在五个数字的排列上,后来发现写出五个数字排列的算法还不如写出验证所合成的五位数的有效性来得简单,于是有了如下的程序:
程序输出的结果如下:
23154 | 23415 | 23451 | 23514 | 23541 | 24135 | 24153 | 24315 | 24351
| 24513 | 24531 | 25134 | 25143 | 25314 | 25341 | 25413 | 25431 |
31245 | 31254 | 31425 | 31452 | 31524 | 31542 | 32145 | 32154 | 32415
| 32451 | 32514 | 32541 | 34125 | 34152 | 34215 | 34251 | 34512 |
34521 | 35124 | 35142 | 35214 | 35241 | 35412 | 35421 | 41235 | 41253
| 41325 | 41352 | 41523 | 41532 | 42135 | 42153 | 42315 | 42351 |
42513 | 42531 | 43125 | 43152 | 43215 | 43251 | 43512 |
sum is: 58
PS:由于我特别粗心大意,不知道程序有没有其他错漏。呵呵,我完成调试的环境是:Mac OS X Leopard 10.5.6 + Safari 3.2.1